désolé ! un peu de physique nécessaire … rassurez vous les 2 dernières parties seront plus simples

Comprendre l’électricité et sa production

3^ème partie – un peu de physique

Un peu de physique que l’on peut « court-circuiter » mais… indispensable si on veut comprendre les bases du courant alternatif, ce que représentent la « puissance active », les « puissances réactives », le « cos(phi) », etc.

Un peu de courage et ça ira tout seul !

1 – Les lois de l’électricité en courant continu

En courant continu, tout est simple. Un seul type de charge, la résistance (R, exprimée en ohms W) et les relations entre la tension U (en volts V), l’intensité électrique I (en ampère A), la résistance R ainsi que la définition de la puissance P (en watts W) sont bien connues :

U=R.I (loi d’Ohm)

P=U.I = R.I²

Le courant circule toujours dans le même sens, du pôle + (cathode) vers le pôle – (anode) selon le sens conventionnel, adopté arbitrairement et qui correspond au sens inverse du déplacement des électrons.Si un courant électrique continu peut engendrer un champ magnétique, celui-ci est constant et donc incapable de générer par induction un courant électrique.Le courant continu peut être produit par les batteries au plomb, les piles électriques, la dynamo, les panneaux photovoltaïques etc.

 

Figure 2 – Lignes ferroviaires :–          Rouge : ligne TGV C. Alternatif 25 kV –          Orange : lignes C. Alternatif 25kV–          Vert : lignes C. Continu 1500V–          Jaune : autres alimentations Si les premiers réseaux électriques fonctionnaient en courant continu, ils ont été rapidement remplacés par le courant alternatif. A Paris, un réseau en courant continu a subsisté jusqu’en 1965 (et à New York jusqu’en 2007 !)

Cependant, une partie du réseau ferroviaire est encore alimentée en courant continu. Sur les 15687 km de lignes électrifiées, 9968 km sont alimentées en 25 kV alternatif mais 5863 km en courant continu 1500 V. Quelques lignes sont également alimentées en courant continu 800 et 850 volts.

2 – l’induction magnétique

Un courant électrique (c’est-à-dire une charge électrique mobile) engendre un champ magnétique (ou plutôt une induction magnétique). Figure 1 – Champ magnétique engendré par un courant électrique circulant dans un circuit en forme de spires De même un flux magnétique variable engendre un courant électrique dans un circuit traversé par ce flux.Ce champ magnétique peut être dû à un aimant permanent (comme dans les dynamos qui équipent les vélos) ou un électroaimant.

 

Figure 2 – Schéma d’un alternateur  Le rotor est constitué d’un aimant permanent et le stator de 3 circuits électriques. La rotation de l’aimant crée au niveau des circuits un champ magnétique variable (variation sinusoïdale) qui induit pour chaque bobine un courant électrique alternatif de même forme !
	Figure 3 – Le transformateur Il est constitué par deux circuits reliés par une armature ferromagnétique (qui concentre et transporte le champ magnétique engendré par le circuit primaire). Si on applique aux bornes du circuit primaire (constitué par n1 spires) une tension U1, il apparaît aux bornes du circuit secondaire (constitué par n2 spires) une tension U2 telle que :

Si U₂ est inférieur à U₁, le transformateur est « dévolteur », sinon il est « survolteur ».

Autre application : la plaque de chauffage par induction

Elle est constituée une bobine qui engendre un champ magnétique haute fréquence qui génère dans la casserole des courants induits (dits « courants de Foucault ») qui chauffent par effet joule.

 

Complément : comment fonctionne l’alternateur ?

Pour comprendre le fonctionnement d’un alternateur il faut se souvenir des notions de base de la trigonométrie.

Considérons le cercle dit « trigonométrique » et un point H qui se déplace sur ce cercle dans le sens « trigonométrique », c’est-à-dire dans le sens inverse des aiguilles d’une montre, à la vitesse angulaire w (« pulsation »)(teta=wt).La projection de H sur l’axe x (OB) est appelé «cosinus q » et la projection sur l’axe y (OC) « sinus teta ». La tangente est définie par OC/OB.

Lorsque le point H se déplace sur le cercle, la projection C sur l’axe y se déplace d’un mouvement de va-et-vient oscillant qui est représenté graphiquement par une courbe sinusoïdale.

Considérons un aimant (soit permanent soit un électroaimant) en rotation autour un axe et 3 circuits électrique fixes à 120° les uns des autres.

Pour le circuit A, le champ magnétique qu’il subit est égal à la composante sur l’axe y du champ magnétique (constant) généré par le pôle + de l’aimant.En effet selon les lois de Laplace seule la composante du champ perpendiculaire au circuit peut agir.

Cette composante du champ a pour intensité H_y=H.sin(teta) dont la variation suit une loi sinusoïdale et va donc générer dans le circuit A une tension de même forme mais uniquement sur une demi-période. Pour la 2^ème demi-période ça sera l’autre pôle (-) qui va induire la tension mais dans le sens opposé (la direction du champ magnétique étant inversée). La tension ainsi générée par la rotation de l’aimant au niveau de la bobine A est donc une sinusoïde complète. Il en sera de même pour les deux autres circuits, générant ainsi 3 tensions alternatives sinusoïdales.

On peut augmenter le nombre d’aimants au niveau du rotor, ce qui permet de réduire la vitesse de rotation du rotor sans changer la fréquence du courant.

Certaines éoliennes utilisent un alternateur (générateur synchrone) dont le rotor est constitué par des aimants permanents de forte aimantation utilisant des terres rares en particulier le néodyme (de l’ordre de 600 kg par éolienne).

3 – Les lois de l’électricité en courant alternatif.

 

Dans un courant alternatif, la variation de la différence de potentielle est de forme sinusoïdale  u=Um.sin(wt)où Um est l’amplitude maximale de la tension, w est la pulsation, w=2(pi)f, f la fréquence et T=1/f la période.En Europe la fréquence est de 50Hz (T=0,2 seconde) et aux USA 60 Hz.

On peut définir une tension et une intensité effectives équivalentes à celles d’un courant continu qui aurait les mêmes propriétés :

1. La résistance purement ohmique

Avec les courants continus, il n’existe qu’une seule charge possible, la résistance R. En courants alternatifs, la résistance se comporte de la même manière et donne les mêmes lois mais avec les valeurs efficaces de la tension et de l’intensité.

Pour une résistance pure, les variations entre la tension et le courant sont en phase·u=Um.sin(wt)·        i=Im.sin(wt) ·        U=RI

En courant alternatif, en plus de la résistance apparaissent deux autres types de charges, la bobine de self-induction et le condensateur.

b)     La bobine de self-inductionUne bobine de self-induction est constituée par un solénoïde (circuit constitué de spires multiples). En courant continu elle se comporte comme une simple résistance mais en courant alternatif le champ magnétique qu’elle engendre va par auto-induction engendrer un courant induit qui s’oppose au courant primaire.

La loi reliant les valeurs efficaces de la tension U et de l’intensité I fait intervenir un terme équivalent à la résistance (bien qu’il n’y ait pas d’effet Joule) mais dépendant de la fréquence, la réactance d’induction, exprimée en ohm :

Z_ind = Lw

Plus la fréquence sera élevée et plus la résistance sera grande. La bobine de self induction représente un filtre pour les hautes fréquences.

.	Dans le cas d’une bobine de self-induction pure, les variations du courant sont en retard par rapport aux variations de la tension, le déphasage est de -pi/2·     u=Um.sin(wt)·     i=Im.sin(wt-pi/2)·     U=Lw.I

1. Le condensateur

En courant continu le condensateur apparaît comme un obstacle, par contre en courant alternatif il se charge et se décharge en permanence. La loi reliant les valeurs efficaces de la tension U et de l’intensité I fait intervenir la réactance de capacité, exprimée en ohm :

Z_capa = 1/Cw

Avec un condensateur les variations du courant sont en avance par rapport aux variations de la tension, le déphasage est de +pi/2·u=Um.sin(wt)·     i=Im.sin(wt+pi/2) ·     I=Cw.U .

Pour le condensateur, contrairement à la self, plus la fréquence est petite et plus la résistance est grande (infinie pour le courant continu).

 

1. L’impédance

Pour un circuit comportant des résistances, des bobines de self-induction et des condensateurs, on peut définir la notion d’impédance (qui joue le même rôle que la résistance en courant continue) :

U=Z.I

Avec :

L’expression de Z n’est que le résultat de l’application de la relation de Pythagore dans la représentation vectorielle des différentes réactances (un déphasage de ±pi/2 se traduisant par une rotation de ±90°)

Représentation vectorielle de l’impédance, somme vectorielle de la résistance et des réactances.

La présence dans le circuit de bobines de self-induction et de condensateurs entraîne un déphasage j entre la tension et le courant :

• u=U_m.sin(wt)
• i=I_m.sin(wt-phi)

 

1. Puissance active, réactive et apparente

En courant continu, la puissance est donnée par la relation P=U.I (=R.I²)

En courant alternatif, cette relation donne la puissance apparente (exprimée en VA, volt-ampère) mais qui n’est pas une puissance réelle.

En fait il faut distinguer la vraie puissance, dite « active » (exprimée en watt), c’est-à-dire celle que l’on peut utiliser directement (sous forme d’énergie mécanique, radiative, thermique…) de la puissance réactive (exprimée en var, volt-ampère-réactif). Cette dernière peut être séparée en deux composantes, la puissance réactive inductive, qui est produite lorsqu’il y a création d’énergie électromagnétique et la puissance réactive capacitive, liée à l’énergie électrostatique.

Le rapport entre la puissance active et la puissance réactive est liée à l’angle de déphasage phi par les relations :

Cos phi est appelé le « facteur de puissance ».

La bobine de self-induction crée de la puissance réactive alors que la capacité en absorbe.

On a donc les définitions des différentes puissances :

• Puissance apparente : S=UI=ZI²
• Puissance active P=UI cos(phi)=RI²
• Puissance réactive : Q=UI sin(phi)

Les relations entre ces différentes puissances peuvent être également représentées comme l’impédance par des vecteurs.

Figure 4 – Représentation vectorielle des différentes puissances. L’introduction d’une puissance réactive capacitive diminue la puissance réactive totale :L’angle phi passe de phi1 à phi2 et le cosinus augmente.

S²=P²+Q²

Seule la puissance active est capable de créer du travail, les autres puissances ne peuvent pas, elles ne sont pas réellement des puissances au sens strict.

Mais avoir de la puissance réactive diminue la puissance active disponible, c’est un handicap à la fois pour le consommateur mais aussi pour le producteur. Pour avoir la même puissance active il faudra augmenter l’intensité du réseau pour compenser la puissance réactive (d’où plus de pertes en ligne pour le producteur et une facture plus importante pour le consommateur).

Dès qu’il est nécessaire de créer un champ magnétique (moteur, lampes fluorescentes, four ou plaque à induction etc.) de la puissance réactive apparaît et le cosj diminue et donc le rendement.

Une manière d’augmenter le cos(phi) est d’ajouter des capacités dans le circuit afin de créer de la puissance réactive capacitive qui compense en partie la puissance réactive inductive.

Si on considère un moteur triphasé développant une puissance active de 500 kW et caractérisé par un cos(phi) égal à 0,7.

En l’absence de compensation, le bilan de puissance est le suivant :

• Puissance active P : 500 kW (utile)
• Puissance réactive Q : 510 kvar (inductif) pour un cos(phi) de 0,7
• Puissance apparente S : 714 kVA (délivrée)

Pour une puissance mécanique du moteur égale à 500 kW, le réseau électrique doit assurer la disponibilité d’une puissance apparente de 714 kVA, soit 143% de la puissance active utile.
En introduisant dans le circuit une batterie de condensateurs pouvant fournir une puissance réactive capacitive de 345 kvar, le bilan de puissance devient :·         Puissance active P : 500 kW (utile)·Puissance réactive Q du moteur: 510 kvar (inductif) ·Puissance réactive capacitive Qc : 345 kvar (capacitif).

 

Après compensation le cos(phi) est passé à 0,95, la puissance réactive résultante n’est plus que de 165 kvar, et la puissance apparente S’ (délivrée) est réduite à 526 kVA

Le réseau d’alimentation ne doit plus fournir qu’une puissance apparente égale à 526 kVA, soit 105% de la puissance active utile. La compensation d’énergie réactive a permis de réduire de 26% la puissance à transmettre (et réduire également d’autant la facture pour l’utilisateur !)

En France tant que Q est inférieur à 40% de P, la puissance réactive n’est pas facturée.

Exemples de cos(phi) pour différents appareils

site d’Electrotech-City – Walter DI PILLA

 

Complément sur le courant triphasé

 

Les tensions sinusoïdales sont déphasées de pi/3 et 2pi/3 (120 et 240°).· · ·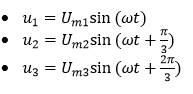

 

Dans un système équilibré les amplitudes sont égales !  U_m1=U_m2=U_m3=U

• La tension efficace entre phases est égale à 
• La tension entre phase et neutre est égale à 

En Europe la tension entre phases est de 380/400 volts d’où une tension entre la phase et le neutre de 220/230 volts.

A partir des 3 conducteurs et éventuellement du conducteur « neutre », deux montages sont possibles, le montage en étoile et le montage en triangle :

	Montage en étoile
	Montage en triangle

 

La puissance disponible en courant triphasé est égale à

Alimentation d’un récepteur en courant triphasé (montage en étoile)

 

Dans un transformateur triphasé, le circuit magnétique est commun aux trois phases. Pour le primaire, deux montages sont possibles, en étoile ou en triangle : pour le secondaire un troisième montage est possible, en « zig-zag ».

 

Transformateur triphasé

Le courant alternatif présente un certain nombre d’avantage que l’on peut résumer ainsi :

• Le transport d’une même puissance électrique en triphasé (sans neutre) nécessite une section de câbles conducteurs deux fois plus faible qu’en monophasé.

L’économie qui en découle sur le coût de réalisation des lignes est notable.

• Les courants triphasés peuvent produire des champs magnétiques tournants en répartissant d’une manière spécifique les bobinages sur un rotor. Or les machines électriques qui produisent et utilisent ces courants fonctionnent de manière optimale en régime triphasé.
• Une distribution de l’électricité en courant triphasé avec fil de neutre permet de proposer pour un même réseau deux tensions d’utilisation différentes :
• soit entre une phase et le neutre : par exemple 230 V en Europe
• soit entre deux phases : par exemple 400 V en Europe